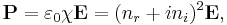Parametric process (optics)
A parametric process is an optical process in which light interacts with matter in such a way as to leave the quantum state of the material unchanged. As a direct consequence of this there can be no transfer of energy, momentum, or angular momentum between the optical field and the physical system. In contrast a non-parametric process is a process in which any part of the quantum state of the system changes.[1]
Contents |
Temporal characteristics
Since a parametric process prohibits a change in the energy state of the system, parametric processes are considered to be 'instantaneous' processes. This can be seen as follows; if an atom absorbs a photon with energy E, the atom's energy will increase by ΔE = E. Since we are assuming this is a parametric process, the quantum state cannot change and thus this energy state must be a Virtual state. By the Heisenberg Uncertainty Principle we know that ΔEΔt~ħ, thus the lifetime of a parametric process is roughly Δt~ħ/ΔE, which is appreciably small for any non-zero ΔE. [1]
Parametric versus non-parametric processes
Linear optics
In a linear optical system the dielectric polarization, P, responds linearly to the presence of an electric field, E, and thus we can write
where ε0 is the electric constant, χ is the (complex) electric susceptibility, and nr(ni) is the real(imaginary) component of the refractive index of the medium. The effects of a parametric process will effect only nr, whereas a nonzero value of ni can only be caused by a non-parametric process.
Thus in linear optics a parametric process will act as a lossless dielectric with the following effects:
Alternatively, non-parametric processes often involve loss (or gain) and give rise to:
- Absorption
- Inelastic scattering
- Various optical emission processes
Nonlinear optics
In a nonlinear media, the dielectric polarization P responds nonlinearly to the electric field E of the light. As a parametric process is in general coherent, many parametric nonlinear processes will depend on phase matching and will usually be polarization dependent.
Sample parametric nonlinear processes:
- Second harmonic generation (SHG), or frequency doubling, generation of light with a doubled frequency (half the wavelength)
- Third harmonic generation (THG), generation of light with a tripled frequency (one-third the wavelength) (usually done in two steps: SHG followed by SFG of original and frequency-doubled waves)
- High harmonic generation (HHG), generation of light with frequencies much greater than the original (typically 100 to 1000 times greater)
- Sum frequency generation (SFG), generation of light with a frequency that is the sum of two other frequencies (SHG is a special case of this)
- Difference frequency generation (DFG), generation of light with a frequency that is the difference between two other frequencies
- Optical parametric amplification (OPA), amplification of a signal input in the presence of a higher-frequency pump wave, at the same time generating an idler wave (can be considered as DFG)
- Optical parametric oscillation (OPO), generation of a signal and idler wave using a parametric amplifier in a resonator (with no signal input)
- Optical parametric generation (OPG), like parametric oscillation but without a resonator, using a very high gain instead
- Spontaneous parametric down conversion (SPDC), the amplification of the vacuum fluctuations in the low gain regime
- Optical Kerr effect, intensity dependent refractive index
- Four-wave mixing (FWM)
- Self-focusing
- Kerr-lens modelocking (KLM)
- Self-phase modulation (SPM), a
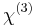effect - Optical solitons
- Cross-phase modulation (XPM)
- Four-wave mixing (FWM), can also arise from other nonlinearities
- Cross-polarized wave generation (XPW), a 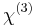effect in which a wave with polarization vector perpendicular to the input is generated
Sample non-parametric nonlinear processes:
- Stimulated Raman scattering
- Raman amplification
- Two-photon absorption, simultaneous absorption of two photons, transferring the energy to a single electron
- Multiphoton absorption
- Multiple photoionisation, near-simultaneous removal of many bound electrons by one photon
See also
Notes
- ^ a b See Section Parametric versus Nonparametric Processes, Nonlinear Optics by Robert W. Boyd (3rd ed.), pp. 13-15.
References
- Boyd, Robert (2008). Nonlinear Optics (3rd ed.). Academic Press. pp. 13–15. ISBN 978-0123694706. http://www.amazon.com/Nonlinear-Optics-Third-Robert-Boyd/dp/0123694701/ref=sr_1_1?ie=UTF8&qid=1313111421&sr=8-1.